First a few words about the two equations that are used in the banner of this site. Both of them are from complex analysis. The following equation \[ B(z) = \prod_{n=1}^{\infty} \frac{z_n}{\left|z_n\right|} \frac{z-z_n}{1-\overline{z_n}z} \] is called a Blaschke product. It is an infinite product which has quite a bit of significance. An analytic function has nice properties in the complex plane. As we know from algebra, we can always construct a function which vanishes at a finite number of points. For instance, suppose we want a function to be zero at $\pm 1$ and $\pm i$. We can accomplish this with the following polynomial: \[ f(z) = (z-1)(z+1)(z-i)(z+i) \]
One can ask a similar question: Can we obtain a function which is zero at infinitely many points? Even better can we do this so that the function is analytic? The answer is yes. This can be done via the Weierstrass factorization. Blaschke products were one of my favorite topics in Complex Analysis.
The other formula is Cauchy's Integral Formula. It is a rather remarkable statement that says one can understand the values of an analytic function by computing the path integral on the right-hand-side. There is no analog to such a statement in real analysis. This formula can be connected to the coefficients in the power series of an analytic function and proofs of the residue theorem, argument principle, etc.
Here's a different look at the two equations:
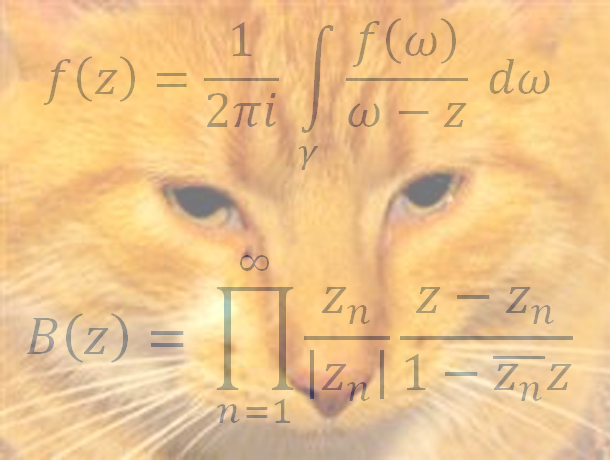
Why do I like math? This question is, in some sense, an easy one for me to answer. Math is compelling to me. Math challenges me on a daily basis. Mathematics allows me to use creativity, tell interesting stories, and have a good time. Tell interesting stories, you ask? I enjoy reading math history and there are many mathematicians who have lead interesting lives: Everiste Galois, Leonhard Euler, and David Hilbert just to name three. When I have fully internalized a concept in mathematics, telling others about it is often about revealing a story. I have often said that research does not happen in a vacuum. It is important to have both a mathematical and historical context to place the ideas, being studied.
Math is Pretty In fact, I had a professor say, "Isn't that pretty?" after completing a proof. There is an innate beauty in mathematics that I love. One of my goals while teaching is to show students some of the artistic quality that is inherent to mathematics. I once told a group of students that I wanted them to be able to "see the Gaughin". By which, I meant that I desired for them to not just understand the symbolism and synthesize the material, but to be able to also find an appreciation. To find, if only for a little part of the study, a facet to explore deeply. I find aesthetic value in a good proof. It is impossible to put into words exactly what a good proof is. For me, often times the proof conveys everything it needs to succinctly, flows well, and perhaps has something a little unexpected. There are certainly many pictures that are used to convey mathematical ideas which are beautiful. Two examples are fractals and projections of Calabi-Yau manifolds.
Why is math so hard? Abstraction is always difficult. Think about one of the first mathematical abstractions that occurs. When we are quite young, we learn how to count on our fingers. It doesn't take long to understand that "five" refers to more than just five fingers. We could pick five apples, eat five sandwiches for lunch, or enjoy five candy bars after lunch. As teenagers, mom wonders if she should have five refrigerators, in order to feed her growing, seemingly always hungry, kids. There is a sense of what "five" is, but applied to unrelated objects. We could have a philosophical discussion and try to nail down exactly what that "sense" is. However, it is exactly this notion that abstraction defies a complete description that makes it useful. The levels of abstraction build on each other, and sometimes in quite subtle ways. A successful math teacher can communicate concrete ideas, abstract ideas, and how they interconnect.
Which brings me to communication. It is unfortunate that some have had the experience of having a math teacher or professor who lacks the necessary communication skills, to be standing in a classroom. The notion that many students get from their mathematical studies is that mathematicians don't write and don't have a need to explain themselves. After all, $x + 2 = 5$, has exactly one solution $x=3$. What more needs to be said? It is actually exactly this question that needs to be asked more often. As mentioned below, we do drill to establish our ability to do techniques. Drill problems lack context, so if that is the case, there probably is not more that needs to be said. On the other hand, if this equation appears in your solution to a word problem, I'm left with a question: So what? You have three of something, what was it that $x$ stood for in the first place? The number of apples you had for snack, the number of refrigerators mom forced dad to buy,...
Words and mathematics actually go hand-in-hand. It is words that hold the symbols together, and not the other way around. When I lecture, I write complete sentences on the board. We are taught that a sentence has a subject and a predicate. As a teacher, I want to make both what is happening and the action taking place clear. There is nothing gained by withholding this information. Students are responsible for communicating what they mean. Proper mathematics is difficult partially because communication is not an easy skill to master.
When in a one-on-one situation with a student, I often have the student do the problem at the board. It is precisely so that the student can use their own words to describe what is happening mathematically that I do this. It's an opportunity to practice communicating what they mean.
True or False: Math is boring! The subject at large is not at all boring. However, there are things in mathematics that are not the most exciting. When I was in 3rd grade, we took out our textbooks, copied problems 13-25 onto a sheet of paper, and performed the indicated operations. This was often met with a lack of excitement. In fact, there came to be a phrase used for this: "drill-and-kill". With such a negative connotation, educators decide to throw out this method of teaching all together and we moved towards teaching "concepts only". The issue with teaching only concepts is it's quite easy to understand the theory and never be able to compute anything. It is unfortunate that mathematics education has lived on such extremes. Drill established both discipline and confidence in using the concepts taught. It is through doing problems that ideas are properly internalized. I have seen a student's frustration overwhelm them quite often. This frustration is often directly connected to the problems they are being asked to do.
Boredom can also take the form of "this course is too easy" for me! When I came back to college, I did not remember any thing from trigonometry. So, when I began my computer engineering program, I took Calculus I and Trigonometry concurrently. The trigonometry course was not at all difficult for me. The problems were immediate for me, and the material wasn't always engaging. Why did I get so much out of it? Just because something is "easy" and "not engaging" does not absolve one of doing it. Neither does it mean we won't get anyting out of the course. The fundamental thing a student must do in such a math course is engage themselves.
Here is the best article I've ever read regarding boredom, self-regulation, and resilience: My 11-year-old son auditioned at Juilliard...
I'll close this section with three thoughts to ponder.
I'm a theorist: I enjoy the process of doing math. I have little concern as to whether or not what I'm studying has a practical application or not. I approach pure math and applied math in exactly the same way. I attempt to understand the answer to an interesting question. As an undergraduate, I felt that I had little use for examples. I typically wanted to try and understand everything in the most general way possible. While I still tend to "live" in the abstraction, four years of graduate school, and many different teaching situations, have made it clear that examples are useful for many reasons. Trying to understand why certain facts are true can be difficult. Proving a theorem can often mean the we're trying to say something about a very large class of mathematical objects. This can lead to feelings of being overwhelmed when it is less than clear as to why the fact is true. Working the statement out for a couple of specific examples often gives one enough insight to see what is happening. Another reason that examples are important is to communicate the ideas. The examples do not need to be deep or difficult. The most important thing is that they convey ideas. As useful as abstraction is, things often become more clear through a couple of well-chosen examples. At the end of the day though, I want to understand the answers to interesting questions, and be around people that want to be a part of intriguing conversation.
Here are some interesting articles: